Справка по площади. виды площадей. единицы измерения площади. конвектор величин единиц измерения площади. калькуляторы площадей

Как посчитать площадь стен

Чтобы определить площадь стен, нужно знать, как рассчитать периметр комнаты. Определение площади часто требуется для закупки всевозможных материалов для отделки. Кроме длины и ширины помещения, понадобится выяснить высоту комнаты, а также габариты проемов двери и окон.

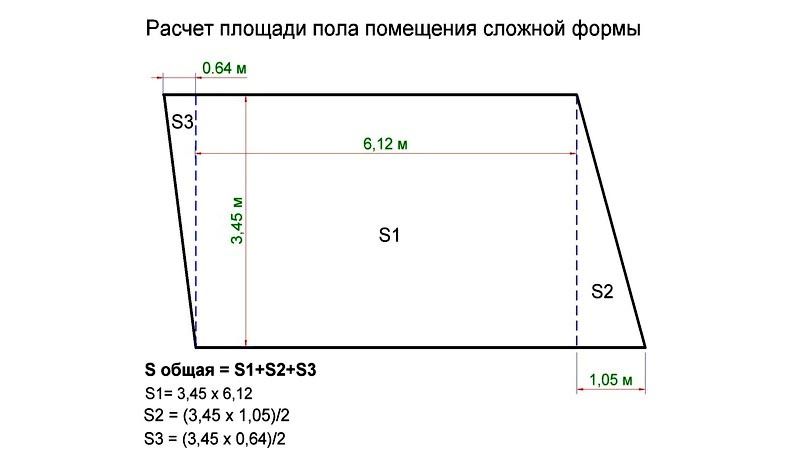Расчет площади стен сложной конфигурации

При расчетах стоит учитывать, что высота потолков даже в одном помещении может варьироваться, особенно если комната мансардного типа. Отдельно вычисляются значения всех стен, а затем их них отнимаются оконные и дверные проемы.

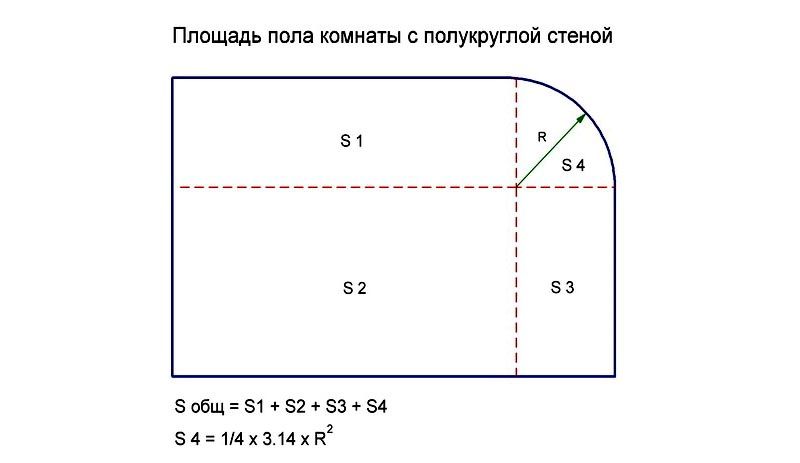Вычисления при полукруглой стене

Точные значения можно выявить с помощью калькулятора расчета площади стен комнаты. Иногда требуется определить объем помещения. В такой ситуации необходимо перемножить три значения: длину, ширину и высоту комнаты. Данный показатель меряется в кубических метрах.

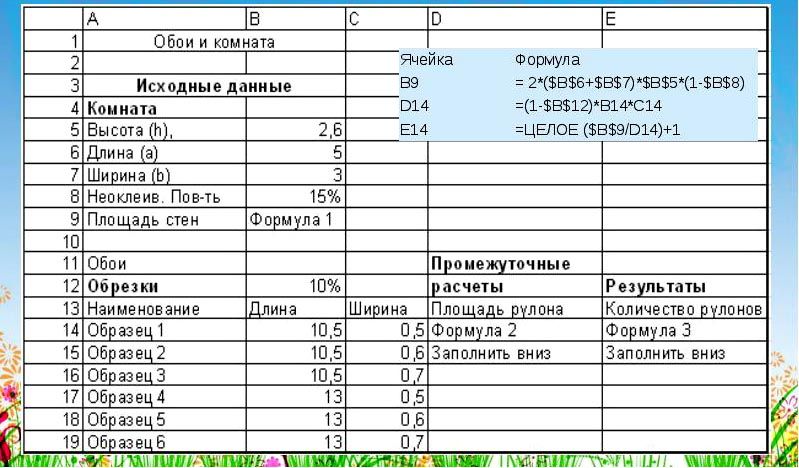Пример расчета обоев с помощью специальной электронной программки

Если помещение имеет разноуровневое зонирование, то можно провести такие расчеты:

• померить все участки стен. Замеры рекомендуется выполнять поближе к потолку;
• вычислить показатели площади по полу;
• на каждом вертикальном участке необходимо промерить длину и высоту, а затем данные значения перемножить;
• прибавьте показатели к значению пола.

У каждой комнаты есть оптимальные параметры, которые можно учитывать при планировке строительного объекта. Минимальный показатель жилого помещения равняется 8 кв. м. Комната общего назначения, такая как зал или гостиная может иметь площадь от 14 до 25 кв. м. Минимальный показатель высоты помещения составляет 240 см. Если потолок более трех метров, то такое пространство сложнее обогревать. Кухня должна иметь площадь не менее 6 кв. м.

Проведение грамотных расчетов позволит создать уютный интерьер даже при сложной конструкции

Правильное вычисление площади помещения является гарантией качественного проведения ремонта. Такой подход позволит свести к минимуму затраты на приобретение материалов.

Как посчитать площадь стен можно посмотреть на видео:

Watch this video on YouTube

Предыдущая РемонтКрасивые и практичные перегородки для зонирования пространства в комнате: 70 идей и советы дизайнеров
Следующая РемонтКак сделать клейстер: технологии и особенности применения

Площадь квадрата

Из младших классов известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.

Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:

Тогда площадь квадрата со стороной 2 равна 4, а со стороной 3 уже равна 9. В общем случае квадрат со стороной n (где n– натуральное число) можно разбить n2 единичных квадратов, поэтому его площадь будет равна n2.

Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:

В общем случае единичный квадрат можно разбить на m2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:

Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.

Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:

Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:

В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине

Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это иррациональное число. Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».

Предположим, что есть некоторое иррациональное число I, такое, что площадь квадрата (S) со стороной I НЕ равна величине I2. Для определенности будем считать, что I22>S, рассматривается абсолютно аналогично). Однако тогда, извлекая корень из обеих частей неравенства, можно записать, что

Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:

Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R2):

из которого следует противоположный вывод – величина R2 меньше, чем S. Полученное противоречие показывает, что исходная утверждение, согласно которому площадь квадрата со стороной I НЕ равна I2, является ошибочным. А значит, площадь квадрата всегда равна его стороне, умноженной на саму себя.

Задание. Найдите площадь квадрата, если его сторона равна

Задание. Площадь квадрата равна 25. Найдите длину его стороны.

Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:

Его простейшее квадратное уравнение, для его решения надо просто извлечь квадратный корень из правой части:

Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.

Задание. Численно площадь квадрата равна периметру квадрата (с учетом того, что площадь измеряется в см2, а периметр – в см). Вычислите его площадь.

Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:

По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:

Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.

Ответ: 16 см2.

Обратите внимание, что ответ задачи зависит от единицы измерения. Если использовать миллиметры, то сторона квадрата окажется равной 40 мм, периметр будет равен 160 мм, а площадь составит 1600 мм2

Именно поэтому в условии задачи сказано, что площадь и периметр равны численно. «По-настоящему» равными бывают только величины, измеряемые в одинаковых единицах измерения.

Виды треугольников

Треугольник представляет собой многоугольник, который имеет три стороны и может быть отнесен к следующим типам:

• Равносторонний треугольник имеет равные стороны и равные углы.
• Равнобедренный треугольник имеет две равные стороны и два равных угла.
• Разносторонний треугольник имеет три неравные стороны и три неравных угла.
• Прямоугольный треугольник имеет один прямой угол 90 градусов.
• Остроугольный треугольник имеет все углы меньше 90 градусов.
• Тупоугольный треугольник имеет один угол больше 90 градусов.

Площадь любого треугольника определяется по формулам.

1. Как рассчитать площадь треугольника, если известны высота и основание треугольника:

• S=1⁄2×a×h, где: h – высота, a — основание.
• S=1⁄2xa×b×sinα, где: a, b – любые две стороны, α — угол между ними.
• S=p×r, где: p = (a+b+c) / 2 — полупериметр, a, b, c – три стороны, r – радиус круга.

Площадь равностороннего треугольника:

S=a2х√3 ⁄4 , где a=b= c.

Площадь равнобедренного треугольника:

S=1⁄4xbx√(4a2-b2).

2. Как рассчитать площадь треугольника, если заданы две стороны и угол между ними:

S=1⁄2xaxbxsinC=1⁄2xbxcxsinA =1⁄2xaxcxsinB.

Пример 1: Найти S треугольника, сторона которого составляет 14 см, а высота — 10 см.

Решение: b=14 см, h=10 см, A=1⁄2х14х10=70

Ответ: 70 см2.

Пример 2. Найти область треугольника, стороны которого и угол между ними заданы следующим образом: a=5 см и b=7 см, C=45 градусов.

Решение: Площадь треугольника =1⁄2xaxbxsin 45.

Площадь =1⁄2×5×7×0,707 (поскольку sin45=0,707)

Площадь =1⁄2×24,745=12,3725

Ответ: 12,3725 см2.

Пример 3. Найдите площадь (в м2) равнобедренного треугольника, стороны которого составляют 10 м, а основание — 12 м.

Решение: Площадь равнобедренного треугольника определяется:

A=1⁄4xbx√(4a2-b2)A=1⁄4х12х√(4х(10)2-(12)2)А=48

Ответ: 48 м2.

Пример 4. Найти площадь треугольника, стороны которого равны 8, 9 и 11 соответственно. Все единицы измерения даны в метрах (м).

Решение: Стороны a=8, b=9 и c=11. Согласно формуле Херона площадь треугольника может быть определена по следующей формуле: A=√(sx(sa)х(sb)х(sc)). Прежде всего нам нужно определить s, которая является полупериметром треугольника: s =1⁄2х(a+b+c)=1⁄2х(8+9+11)=14.

Теперь, вставив значение полупериметра в формулу Герона, можно определить площадь треугольника: A=√(sx(sa)х(sb)х(sc)). A=√(14х(14-8)х(14-9)х(14-11)). A=√(1260)=35,50

Ответ: 35,50 м2.

Пошаговый расчет площади комнаты

Шаг 1. Первым делом необходимо приготовить все измерительные инструменты, а также листок и ручку. На бумаге можно предварительно начертить схему комнаты, стараясь максимально сохранить геометрию и отобразить все ниши и детали помещения. Рулетка используется максимально длинная.

Подготовка всего необходимого

Шаг 2. Измеряется длина комнаты. Если она настолько велика, что рулетки не хватает, то замеры снимаются поэтапно. Для начала производится замер на максимальную длину рулетки, в месте ее окончания делается отметка, от которой потом снова производится замер до конца комнаты.

Для начала нужно измерить длину комнаты

Шаг 3. Измеряется ширина комнаты (вдоль стены с меньшей длиной). Рулетка располагается под прямым углом к ранее измеряемой стене комнаты (длине). Полученные данные записываются.

Измеряется ширина комнаты

Шаг 4. Полученные показатели перемножаются между собой. Для этих целей рекомендуется использовать калькулятор. При необходимости значение площади округляется в большую сторону.

Полученная цифра округляется в большую сторону

Шаг 5. Если необходимо измерить площадь сложной геометрически комнаты, то для начала сложная фигура делится на несколько простых – квадратов, треугольников, прямоугольников. Объект изображается на листочке бумаги схематически, схематически делится.

Комната разделена на 4 прямоугольника

Шаг 6. Производится замер каждой фигуры в отдельности. Например, прямоугольники, треугольники.

Каждая фигура замеряется отдельно

Шаг 7. Производится вычисление площади каждой фигуры. Далее все полученные значения суммируются и получается полная точная площадь пола комнаты.

Пример расчета площади треугольника

Методика выполнения работы

Перед тем, как рассчитать квадратуру дома, нужно подготовить следующее:

1. Калькулятор для проведения вычислений. 
2. Рулетка для проведения измерений. При этом надо учитывать, что некоторые производят измерения в дюймах – они не подойдут. Нужна рулетка, которая указывает длину с помощью сантиметров. 
3. Потребуется план квартиры. Измерение площади стен, пола и потолка будет выполняться на его основе. Если такую схему найти нельзя, то её нужно нарисовать от руки, стремясь реалистично отобразить размеры и геометрическую форму частей. 
4. Также потребуется бумага и карандаш для ведения записей в процессе работы. 

При замерах полов, стен и потолков в первую очередь потребуются знания из школьной геометрии. Простейшим способом, как рассчитать площадь дома в квадратных метрах, является вычисление прямоугольных поверхностей. Площадь прямоугольника вычисляется как произведение его сторон. 

Вычисление площади простейших геометрических фигур основано на базовых формулах из геометрииИсточник stroychik.ru

При этом важно учитывать следующее.

Хотя на вид комната состоит из прямоугольных деталей, на самом деле это может оказаться немного по-другому. Например, ширина стен, измеренная с одной и другой стороны, может отличаться на несколько сантиметров. Эта проблема особенно существенна при измерении расстояний в домах старой постройки. В таких случаях обычно измеряют длину в нескольких местах, а при вычислении площади используют среднее значение. 
Вычисления позволяют получить нужные цифры с высокой точностью

Однако будет разумной предосторожностью при вычислениях добавить к площади небольшую величину. Это позволит исключить ситуацию, в которой стройматериалов чуть-чуть не хватило. 

Таким способом можно вычислить площадь прямоугольных пустых стен, пола и потолка.
 

Сложная форма стен и потолка может быть разделена на простые фигуры для упрощения вычисленийИсточник www.buvbaze.lv

Расчёт площади стен с окнами и дверьми

Если на стене есть окно или дверь, то вычисление производится следующим образом:

• Определяется площадь стены без учёта двери или окна. 
• Вычисляется площадь каждого окна или двери путём умножения их длины на ширину. 
• Из площади стены вычитают площадь окон и дверей. 

Этот способ применим в тех случаях, когда рассматриваются прямоугольные стены.

Площадь стены, имеющей неправильную форму

В этом случае нужно разделить вычисления на этапы. Стена с нишами может иметь сложную форму. Однако её всегда можно условно разбить на несколько участков, каждый из которых соответствует одной из простых форм. Затем надо рассчитать площади каждой из частей и сложить их. 

Как посчитать площадь стен, рассказано в видео

Расчёт через периметр

Если комната имеет неправильную форму, то площадь стен можно вычислить, измерив длину периметра. В этом случае проводят измерение горизонтальных отрезков по каждой из сторон помещения и складывают их вместе, затем определяют высоту. Произведение этих величин равно площади стен в этом помещении. 

Несколько советов

• Нужно при проведении расчётов все цифры наносить на план. Таким образом сохранится не только результат, но и промежуточные вычисления, которые могут пригодится при проведении ремонтных работ в будущем. 
• При вычислении площади нужно учитывать, что не всегда необходима полная величина. Например, обои могут клеить не только на всю стену, а на их часть. Класть плитку могут до потолка либо только до определённой высоты. Поэтому нужно точно определить, как высчитать квадратуру дома с учётом конкретного плана ремонта. 

Как сделать замеры – можно посмотреть в видеоролике:

Для того, чтобы точно знать, сколько необходимо стройматериалов для проведения работ, нужно учитывать площади стен, пола и потолка, а также нормы расхода стройматериалов. Среднюю величину расхода можно узнать, спросив у продавцов, а квадратуру дома необходимо измерить самостоятельно. Для этого нужно воспользоваться знаниями из элементарной геометрии. При вычислении площади сложных фигурных поверхностей их разбивают на простые части, делают необходимые вычисления, затем суммируют их. 

Как рассчитать площадь комнаты стандартной формы

Под площадью комнаты подразумеваются числовые характеристики, которые показывают её размер в двухмерном пространстве. Если комната стандартная (прямоугольная или квадратная), то сделать расчёт легко. Нужно только померить длину и ширину. Делается это вдоль стен по полу, при загроможденности данных участков, возможно, проводить замер посредине комнаты.

Важно, одна сторона должна измеряться строго перпендикулярно второй. Стороны расположенные параллельно должны иметь один размер, но несмотря на это, меряются обе

Кроме того, следует проверить правильность формы, то есть провести промеры диагоналей. В прямоугольном или квадратном помещении, они должны равняться, или иметь небольшие отклонения.

Квадратное помещение

Как рассчитать S квадратных помещений — это довольно легко. У квадратной комнаты все стороны равны.  Однако, как говорилось выше, надо замерить их все, и взять средне арифметический показатель для расчёта:

А — размер сторон.

Рассмотрим пример: комната со стенами по 3 метра, 3 в квадрате — S = 9 м2.

Прямоугольное

Рассчитать площадь помещений прямоугольной конфигурации, также легко путём следующих вычислений:

На примере видно, при ширине 4,10 м, длине 6,15 м, S комнаты получается — 4,10 x 6,15 = 25,215 м2. После запятой оставляется две цифры, остальные округляются, то есть выходит 25,22 м2.

Как подготовиться к расчетам

Проведение подготовительных манипуляций заключается в подготовке места для измерений. Также необходимо подготовить инструмент и специальные принадлежности. Лучше если комната будет свободной от посторонних предметов. Часто такое случается при замерах в новом доме или во время проведения ремонта. Замеры длины сторон производятся вдоль стенок. При этом нужно освободить хотя-бы участки, для свободного проведения рулеткой. Результаты замеров можно сразу же перенести на схему. Обязательно следует проверить прямоугольности комнаты. Для этого выполняется замер диагональных линий.

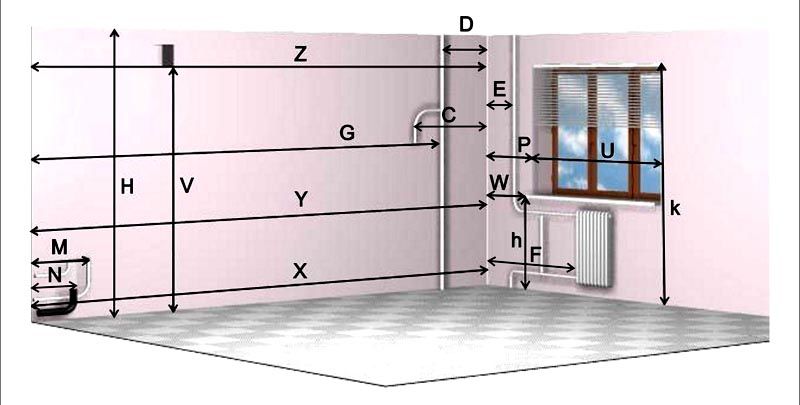Особенности замеров с учетом линий коммуникаций

Кроме рулетки вам может понадобиться специальная линейка для проверки прямых линий. Это может быть строительный уровень или правило. Иногда необходим строительный угольник больших размеров. Как вариант, самодельный циркуль. Можно использовать кусок шнура, привязанный к острому штырю. Для пола можно использовать специальные принадлежности для замеров. Для этого подойдет маркер, мел или скотч. Замеры выполняйте несколько раз. Это позволит избежать ошибки. Следите, чтобы лента для проведения замеров не провисала. Помните, что на многие измерительные инструменты наносится две шкалы. Нельзя путать метрическую систему и дюймовую.

Лазерное приспособление заметно облегчает работу

Перед замерами набросайте простой план – схему на бумаге. Это позволит правильно распределить все замеры. Стоит учитывать, что многие формулы расчетов очень сложные. В этом случае посчитать в столбик не получится. Чтобы посчитать без ошибок, можно воспользоваться программой Excel.

На схеме показаны все необходимые замеры для правильных расчетов

Квадрат

Площадь квадрата определяют как вторую степень длины стороны:

Доказательство вытекает из определения, согласно которому квадратом называют прямоугольник. У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.

Площадь квадрата можно найти другим способом, например, если использовать диагональ:

Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной окружностью? Для расчета площади формулы такие:

1. Через радиус окружности r. Для площади круга вычисление можно сделать следующим образом:
2. Через диаметр окружности d. Найти площадь круга можно так:

Параллелограмм

Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение. Если же высота неизвестна, то тогда как найти площадь параллелограмма? Есть еще один способ вычисления. Потребуется определенное значение, которое примет тригонометрическая функция угла, образованного смежными сторонами, а также их длины.

Формулы площади параллелограмма таковы:

Виды треугольников

Треугольник представляет собой многоугольник, который имеет три стороны и может быть отнесен к следующим типам:

• Равносторонний треугольник имеет равные стороны и равные углы.
• Равнобедренный треугольник имеет две равные стороны и два равных угла.
• Разносторонний треугольник имеет три неравные стороны и три неравных угла.
• Прямоугольный треугольник имеет один прямой угол 90 градусов.
• Остроугольный треугольник имеет все углы меньше 90 градусов.
• Тупоугольный треугольник имеет один угол больше 90 градусов.

Площадь любого треугольника определяется по формулам.

1. Как рассчитать площадь треугольника, если известны высота и основание треугольника:

• S=1⁄2×a×h, где: h – высота, a — основание.
• S=1⁄2xa×b×sinα, где: a, b – любые две стороны, α — угол между ними.
• S=p×r, где: p = (a+b+c) / 2 — полупериметр, a, b, c – три стороны, r – радиус круга.

Площадь равностороннего треугольника:

S=a2х√3 ⁄4 , где a=b= c.

Площадь равнобедренного треугольника:

S=1⁄4xbx√(4a2-b2).

2. Как рассчитать площадь треугольника, если заданы две стороны и угол между ними:

S=1⁄2xaxbxsinC=1⁄2xbxcxsinA =1⁄2xaxcxsinB.

Пример 1: Найти S треугольника, сторона которого составляет 14 см, а высота — 10 см.

Решение: b=14 см, h=10 см, A=1⁄2х14х10=70

Ответ: 70 см2.

Пример 2. Найти область треугольника, стороны которого и угол между ними заданы следующим образом: a=5 см и b=7 см, C=45 градусов.

Решение: Площадь треугольника =1⁄2xaxbxsin 45.

Площадь =1⁄2×5×7×0,707 (поскольку sin45=0,707)

Площадь =1⁄2×24,745=12,3725

Ответ: 12,3725 см2.

Пример 3. Найдите площадь (в м2) равнобедренного треугольника, стороны которого составляют 10 м, а основание — 12 м.

Решение: Площадь равнобедренного треугольника определяется:

A=1⁄4xbx√(4a2-b2)A=1⁄4х12х√(4х(10)2-(12)2)А=48

Ответ: 48 м2.

Пример 4. Найти площадь треугольника, стороны которого равны 8, 9 и 11 соответственно. Все единицы измерения даны в метрах (м).

Решение: Стороны a=8, b=9 и c=11. Согласно формуле Херона площадь треугольника может быть определена по следующей формуле: A=√(sx(sa)х(sb)х(sc)). Прежде всего нам нужно определить s, которая является полупериметром треугольника: s =1⁄2х(a+b+c)=1⁄2х(8+9+11)=14.

Теперь, вставив значение полупериметра в формулу Герона, можно определить площадь треугольника: A=√(sx(sa)х(sb)х(sc)). A=√(14х(14-8)х(14-9)х(14-11)). A=√(1260)=35,50

Ответ: 35,50 м2.

4 Как рассчитать квадратуру стен

Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:

• высота потолков;
• высота и ширина дверных проемов;
• высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.

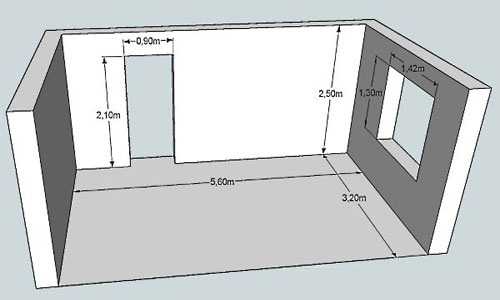Удобнее всего размеры наносить на план

Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.

1. Стена с дверью:
   • 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
   • сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
   • стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
2. Стена с окном:
   1. квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
   2. сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,85 кв.м.
   3. стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.

Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.

4.1 Как измерять стены с дверью и окном?

Если в комнате есть окно или дверь, то для получения актуальных показателей их необходимо обязательно измерить. Воспользовавшись все той же рулеткой, узнайте высоту и ширину оконного проема, умножьте один результат на другой и вычтите это произведение из общей площади. Не надейтесь на то, что их форма является правильной.

Приведем пару примеров.

Пример 1. Стена с дверным проемом:

• Общая S стены – 2,7 м х 8,0 м = 21,6 м2;
• S дверного проема в стене – 2,3 м х 0,9 м = 2,07 м2;
• S стены без дверей – 21,6 м2 – 2,07 м2 = 19,53 м2.

Пример 2. Стена с оконным проемом:

• Общая S стены – 2,4 м х 5 м = 12 м2;
• Площадь окна – 1,4 м х 1,65 м = 2,24 м2;
• S стены без окна – 12 м2 – 2,24 м2 = 9,76 м2.

4.2 Что нужно, чтобы рассчитать площадь стен?

Рассчитать площадь стен дома можно либо онлайн, либо вручную. Второй вариант более трудоемкий, но точный и подходит в случае, если нет доступа к интернету по тем или иным причинам. Для расчетов потребуется:

• карандаш или ручка;
• листок бумаги;
• калькулятор;
• длинная линейка;
• уровень;
• рулетка.

Важно! Зная точную площадь стен и помещения, можно приобрести нужное количество строительных материалов, необходимых для ремонта. Площадь измеряют квадратными метрами и обозначают м2

На бумаге делается чертеж комнат, обозначаются окна, двери, ниши, все выступы. И по мере получения замеров, их наносят на чертеж.

4.3 Как посчитать квадратные метры стены с окном

Сложнее будет иметь дело со стеной, на которой расположено окно.

В таком случае надо отдельно высчитать размер стены, отдельно – размер окна. Потом из большей площади вычесть меньшую. Получится число метров квадратных, которое необходимо будет покрыть краской или штукатуркой.

Алгоритм действий:

1. По уже пройденному сценарию высчитать размер стены. Пускай будет уже известное число – 15,4 м2.
2. Далее измерить высоту и длину окна. Перемножить числа. К примеру: длина 1,5 м, высота 1,2 м. Если умножить, то получится 1,8. Значит, площадь окна 1,8 кв. м.
3. Берем площадь стены и вычитаем из нее размер окна: 15,4 – 1,8 = 13,6. Площадь, которую необходимо будет привести в порядок, – 13,6 кв. м.

Важно! Цифры, которые получаются при подсчетах, обязательно записывать и обводить ручкой, чтобы не потеряться в собственных расчетах

4.4 Как посчитать квадратные метры стены с дверью

Похожие действия необходимо производить, когда требуется высчитать квадратные метры стены с дверью. Если дверь с математической точки зрения простой прямоугольник, то вычисляем ее площадь по обычной формуле А X В. То есть надо измерить высоту и длину, далее числа перемножить и получится размер двери.

Далее из площади стены вычитаем размер двери и получаем квадратуру, на которую необходимо будет покупать отделочные материалы. Если предыдущий хозяин квартиры сделал дверь с аркой, то здесь без вычисления размера круга никак не обойтись.